 |
請輸入關鍵字 |
|
|
| 聯系我們 |
江蘇恒大儀表有限公司
地 址:江蘇省金湖工業園區
郵 編:211600
電 話:0517-86500336
86500226
傳 真:0517-86800636
聯系人:楊經理
手機:13915187193(微信同號)
E-mail:jshdyb@163.com
|
|
|
渦街流量計的標定誤差來源分析 |
|
| 發布日期:2021-06-17 點擊:1707次 |
渦街流量計本質上是一種速度式流量計,其直接測量的量為介質的流速,考慮到由于體積流量僅以介質流速及截面積確定,不受其他因素影響,因此,一般以體積流量進行示值誤差或儀表系數的計算依據。
在使用文丘里噴嘴氣體流量標準裝置對流量計進行標定時,根據連續性原理,達到臨界條件后,只要分別測得被檢流量計、噴嘴兩處的氣體溫度、靜壓、濕度,則可通過密度關系計算被檢表處流量標準值,即標準裝置示值,再讀取流量計示值即可計算示值誤差。但如上文所示的流量計一般無法直接測量其內部氣體狀態參數,而只能在儀表上、下游的管道上進行開孔測量作近似估值,通過此方式所測流量標準值實際為測量孔截面處氣體流量。考慮到在實驗室條件下,氣體的溫度、濕度基本恒定,而在不同的位置測量的靜壓值則有較大差異,因此,測壓位置的選取對體積流量標準值的計算準確性起重要影響。根據JJG1029-2007《渦街流量計檢定規程》,一般于儀表下游段2至7倍內徑距離的范圍內都可認為是合理的測壓位置,所測靜壓與儀表內部實際值近似視作相等,但當被檢儀表為上文所述E+H流量計時,由于其表體管道內徑稍大于標準裝置管道,則儀表與直管段間連接處將出現突變轉折截面,如圖4所示,當氣體流經轉折面時,將產生一定壓力損失,此時下游段測壓處所測得氣體靜壓理論上比儀表內部實際值小,導致計算所得標準體積流量比儀表處實際值大,且流量越大該過程的壓能損失越多,下游測壓計算所得標準值越偏離真值,這種誤差可認為是實驗方法引起的系統誤差[6]。
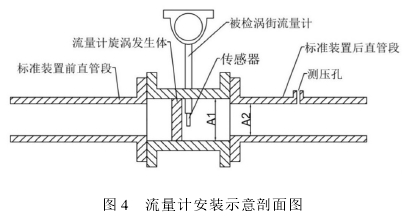
4.1機械能損失分析
因流量計傳感器組成部分前后均有一定長度表體直管段且與標準裝置管道間內徑差異較小,流場擾動基本被儀表本身抗干擾能力克服,可認為流量計計量性能不受影響,則只需考慮氣體靜壓測量值的準確性。從能量損失角度分析:如圖5所示,由于流線不能轉折,流體在流經突然收縮斷面時,將形成流股收縮,至c-c斷面后逐漸擴散,在此過程中,流體先有加速的收縮流后減速的擴散流兩者都產生阻力[7]。為簡化分析此過程中的能量損失,設流體為不可壓縮流體,設c-c斷面處的理想平均流速為v0,根據伯努利方程:
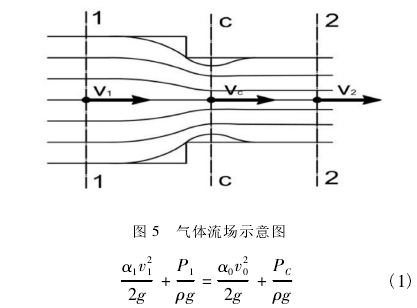
式中,α1為動能修正系數,無量綱;v1為斷面1-1處流體平均流速,m/s;P1為斷面1-1處流體靜壓,N/m2;α0為動能修正系數,無量綱;v0為斷面c-c處流體理想平均流速,m/s;PC為斷面c-c處流體靜壓,N/m2;ρ為流體密度,kg/m3;g為重力加速度,N/kg或m/s2。
實際上從1-1斷面至c-c斷面間存在一定能量損失,假設為U1,再者c-c斷面的實際平均流速νC要比v0稍小一些,它們的比值νC/v0=Cν,稱為流速系數,一般約為0.99~0.97[7],基于本文所討論情況,該斷面收縮較小,取Cν=0.99計算,且在紊流狀態下α1=α0=1,即:


由于在標定實驗中,流體介質一般為空氣,而空氣是一種可壓縮流體,考慮到在重力場中,可壓縮性流體的勢能與壓力能、動能比較起來是小得可以忽略不計的[7-8],即伯努利方程可簡化為以下形式:
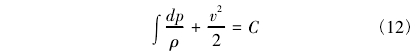
其中C為常數,且氣體在流量計內(斷面1-1處)流至測壓處(斷面2-2)的過程中可近似地看作等熵過程,因此,有P1/ρk1=P2/ρk2,ρ1=P1/P2()1/kρ2,對于空氣的等熵指數k≈1.4,由于在此過程中單位質量流體的能量損失U很小,為簡化分析直接用ρ2計算其機械能損失,則方程可寫為:
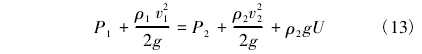
式中,P1為渦街流量計內(斷面1-1處)空氣靜壓,N/m2;ρ1為流量計內(斷面1-1處)空氣密度,kg/m3;v1為流量計內(斷面1-1處)空氣平均流速,m/s;P2為測壓點(斷面2-2處)空氣靜壓,N/m2;ρ2為測壓點(斷面2-2處)空氣密度,kg/m3;v2為流量計內(斷面2-2處)空氣平均流速,m/s。
由于在標定實驗中,空氣的質量流量Qm可通過文丘里噴嘴測量換算得到,設斷面1-1處、斷面2-2處管道面積為S1、S2,則空氣在兩處的流速分別為:
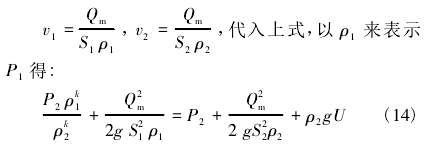
式中,Qm為空氣的質量流量,kg/s;S1為斷面1-1管道截面積,m2;S2為斷面2-2管道截面積,m2。
經過變換得到一個一元方程,僅有ρ1為未知量,各項參數均能在實驗中直接測量或換算所得,通過使用軟件工具如MATLAB、Excel或其他方式解出ρ1,則P1=P2ρk1/ρk2,流量計內體積流量的理論值QV為:
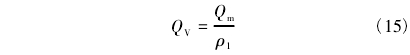
式中,QV為空氣的體積流量,m3/s。 |
 |
相關新聞: |
 |
|
|


